The chi-square test of independence is used to determine whether two or more samples of cases differ on a nominal level variable. A Pearson correlation is used to determine the relationship between two continuous variables
The chi-square test of independence is used to determine whether two or more samples of cases differ on a nominal level variable.
Application of the Pearson Correlation and Chi–Square Test
The chi–square test of independence is used to determine whether two or more samples of cases differ on a nominal level variable. A Pearson correlation is used to determine the relationship between two continuous variables. Both the chi–square test of independence and correlation are widely used in the analysis of public health data.
The purpose of this assignment is to practice calculating and interpreting the Pearson correlation coefficient and a chi–square test of independence. After analyzing the data, communicate the results of one of the tests in a PowerPoint presentation. Refer to the Using and Interpreting Statistics: A Practical Text for the Behavioral, Social, and Health Sciences textbook and instructional videos for assistance completing this assignment.
Part 1
Use SPSS “Health Behavior Data Set” and complete the following:
- Conduct a Pearson correlation to determine the relationship between age and annual income.
- Conduct a chi–square test to determine the relationship between sex and smoking status.
- Export the SPSS output for the Pearson correlation and chi-square tests.
Part 2
Create an 8-10-slide PowerPoint presentation to discuss the findings of the chi-square or correlation. Create a voice-over or a video presentation that is 5-7 minutes in length. Your slides should be shown on the screen as you present. Loom may be used (you must use your GCU email address to access all of the features for Loom). Other options are Zoom or the recording feature in PowerPoint. Include an additional slide for the link with your selected method of presentation at the beginning and an additional slide for references at the end.
Include the following.
Include the following:
- Explain why the statistical test is most appropriate for analyzing the data and whether the assumptions were met.
- What are the null and alternative hypotheses for this specific scenario?
- What is the critical value? What is the decision rule?
- Per the output, what is the test statistic and p-value?
- How do you interpret the results? (What was done? What was found? What does it mean? What suggestions are there for the creation of a health promotion intervention?)
General Requirements
Submit the SPSS exported output (Part 1) and the PowerPoint presentation (Part 2) to the assignment dropbox.
While APA style is not required for the body of this assignment, solid academic writing is expected, and documentation of sources should be presented using APA formatting guidelines, which can be found in the APA Style Guide, located in the Student Success Center.
This assignment uses a rubric. Please review the rubric prior to beginning the assignment to become familiar with the expectations for successful completion.
You are required to submit this assignment to LopesWrite. A link to the LopesWrite technical support articles is located in Class Resources if you need assistance.
Expert Answer and Explanation
Part 1 – Write Up
GET DATA
/TYPE=XLSX
/FILE=’C:\Users\PRIMERA\Downloads\PUB-550-RS-T2-T3-T4-HealthBehaviorDataset.xlsx’
/SHEET=name ‘Data’
/CELLRANGE=FULL
/READNAMES=ON
/DATATYPEMIN PERCENTAGE=95.0
/HIDDEN IGNORE=YES.
EXECUTE.
DATASET NAME DataSet2 WINDOW=FRONT.
CORRELATIONS
/VARIABLES=Age Annual_Income
/PRINT=TWOTAIL NOSIG FULL
/MISSING=PAIRWISE.
Correlations
| Notes | ||
| Output Created | 20-APR-2025 05:01:17 | |
| Comments | ||
| Input | Active Dataset | DataSet2 |
| Filter | <none> | |
| Weight | <none> | |
| Split File | <none> | |
| N of Rows in Working Data File | 32 | |
| Missing Value Handling | Definition of Missing | User-defined missing values are treated as missing. |
| Cases Used | Statistics for each pair of variables are based on all the cases with valid data for that pair. | |
| Syntax | CORRELATIONS
/VARIABLES=Age Annual_Income /PRINT=TWOTAIL NOSIG FULL /MISSING=PAIRWISE. |
|
| Resources | Processor Time | 00:00:00.03 |
| Elapsed Time | 00:00:00.02 | |
| Correlations | |||
| Age | Annual_Income* | ||
| Age | Pearson Correlation | 1 | .139 |
| Sig. (2-tailed) | .463 | ||
| N | 30 | 30 | |
| Annual_Income* | Pearson Correlation | .139 | 1 |
| Sig. (2-tailed) | .463 | ||
| N | 30 | 30 | |
CORRELATIONS
/VARIABLES=Age Annual_Income
/PRINT=TWOTAIL NOSIG FULL
/CI CILEVEL(95)
/MISSING=PAIRWISE.
Correlations
| Notes | ||
| Output Created | 20-APR-2025 05:03:48 | |
| Comments | ||
| Input | Active Dataset | DataSet2 |
| Filter | <none> | |
| Weight | <none> | |
| Split File | <none> | |
| N of Rows in Working Data File | 32 | |
| Missing Value Handling | Definition of Missing | User-defined missing values are treated as missing. |
| Cases Used | Statistics for each pair of variables are based on all the cases with valid data for that pair. | |
| Syntax | CORRELATIONS
/VARIABLES=Age Annual_Income /PRINT=TWOTAIL NOSIG FULL /CI CILEVEL(95) /MISSING=PAIRWISE. |
|
| Resources | Processor Time | 00:00:00.03 |
| Elapsed Time | 00:00:00.02 | |
Confidence Intervals |
||||
| Pearson Correlation | Sig. (2-tailed) | 95% Confidence Intervals (2-tailed)a | ||
| Lower | Upper | |||
| Age – Annual_Income* | .139 | .463 | -.233 | .476 |
| a. Estimation is based on Fisher’s r-to-z transformation. |
CROSSTABS
/TABLES=Sex BY Smoker
/FORMAT=AVALUE TABLES
/CELLS=COUNT
/COUNT ROUND CELL.
Crosstabs
| Notes | ||
| Output Created | 20-APR-2025 05:06:59 | |
| Comments | ||
| Input | Active Dataset | DataSet2 |
| Filter | <none> | |
| Weight | <none> | |
| Split File | <none> | |
| N of Rows in Working Data File | 32 | |
| Missing Value Handling | Definition of Missing | User-defined missing values are treated as missing. |
| Cases Used | Statistics for each table are based on all the cases with valid data in the specified range(s) for all variables in each table. | |
| Syntax | CROSSTABS
/TABLES=Sex BY Smoker /FORMAT=AVALUE TABLES /CELLS=COUNT /COUNT ROUND CELL. |
|
| Resources | Processor Time | 00:00:00.03 |
| Elapsed Time | 00:00:00.01 | |
| Dimensions Requested | 2 | |
| Cells Available | 524245 | |
Case Processing Summary |
||||||
| Cases | ||||||
| Valid | Missing | Total | ||||
| N | Percent | N | Percent | N | Percent | |
| Sex * Smoker | 32 | 100.0% | 0 | 0.0% | 32 | 100.0% |
CROSSTABS
/TABLES=Sex BY Smoker
/FORMAT=AVALUE TABLES
/STATISTICS=CHISQ
/CELLS=COUNT EXPECTED
/COUNT ROUND CELL.
Crosstabs
| Notes | ||
| Output Created | 20-APR-2025 05:13:30 | |
| Comments | ||
| Input | Active Dataset | DataSet2 |
| Filter | <none> | |
| Weight | <none> | |
| Split File | <none> | |
| N of Rows in Working Data File | 32 | |
| Missing Value Handling | Definition of Missing | User-defined missing values are treated as missing. |
| Cases Used | Statistics for each table are based on all the cases with valid data in the specified range(s) for all variables in each table. | |
| Syntax | CROSSTABS
/TABLES=Sex BY Smoker /FORMAT=AVALUE TABLES /STATISTICS=CHISQ /CELLS=COUNT EXPECTED /COUNT ROUND CELL. |
|
| Resources | Processor Time | 00:00:00.02 |
| Elapsed Time | 00:00:00.03 | |
| Dimensions Requested | 2 | |
| Cells Available | 524245 | |
Case Processing Summary |
||||||
| Cases | ||||||
| Valid | Missing | Total | ||||
| N | Percent | N | Percent | N | Percent | |
| Sex * Smoker | 32 | 100.0% | 0 | 0.0% | 32 | 100.0% |
Sex * Smoker Crosstabulation |
||||||
| Smoker | Total | |||||
| No | Yes | |||||
| Sex | Count | 2 | 0 | 0 | 2 | |
| Expected Count | .1 | 1.1 | .8 | 2.0 | ||
| Female | Count | 0 | 8 | 7 | 15 | |
| Expected Count | .9 | 8.4 | 5.6 | 15.0 | ||
| Male | Count | 0 | 10 | 5 | 15 | |
| Expected Count | .9 | 8.4 | 5.6 | 15.0 | ||
| Total | Count | 2 | 18 | 12 | 32 | |
| Expected Count | 2.0 | 18.0 | 12.0 | 32.0 | ||
| Chi-Square Tests | |||
| Value | df | Asymptotic Significance (2-sided) | |
| Pearson Chi-Square | 32.593a | 4 | .000 |
| Likelihood Ratio | 15.520 | 4 | .004 |
| N of Valid Cases | 32 | ||
| a. 5 cells (55.6%) have expected count less than 5. The minimum expected count is .13. |
Part 2 – Powerpoint Presentation

Welcome! This presentation applies the chi-square test of independence to public health data. The analysis explores the relationship between sex and smoking status using SPSS and the Health Behavior Dataset. The goal is to determine if smoking behavior is statistically related to sex. This type of analysis helps public health professionals target interventions and better understand population health behaviors. The chi-square test is ideal for nominal-level variables, such as gender and smoking status, which are categorical in nature. Let’s review the test rationale, hypotheses, results, and implications for health promotion strategies.

The chi-square test of independence was chosen because both variables—sex and smoking status—are nominal. This test helps us determine whether there’s a statistically significant relationship between these two variables (Miola & Miot, 2022). Specifically, we ask whether the distribution of smokers is different between males and females. This test is widely used in public health because many important variables are categorical (Miola & Miot, 2022). Understanding this relationship can guide targeted health communication or prevention campaigns, such as smoking cessation efforts based on gender patterns.

This slide presents the Pearson correlation between age and annual income. The correlation coefficient is r = .139, indicating a very weak positive relationship. The p-value = .463, which is greater than .05, means the result is not statistically significant. Therefore, we fail to reject the null hypothesis.
Before conducting the analysis, we verified key assumptions:
- Both age and annual income are continuous variables.
- A scatterplot showed no strong linear trend, confirming the weak correlation.
- We checked for normal distribution, which appeared approximately normal given the small sample size.
- There were no extreme outliers that could distort the correlation.
The SPSS output table shown here displays all essential values: the correlation, significance level, and sample size (N = 30). Overall, there’s no meaningful linear relationship in this sample.

The hypotheses are clearly defined. The null hypothesis (H₀) assumes that smoking status is independent of sex. In contrast, the alternative hypothesis (H₁) suggests that there is a significant association between these variables. Our goal is to analyze the data and determine whether there is enough evidence to reject the null hypothesis in favor of the alternative. A statistically significant result would indicate that sex influences smoking behavior in this dataset.

To determine if our test is statistically significant, we compare the test statistic to the critical value (Aguinis et al., 2021). At α = 0.05 and df = 4, the critical chi-square value is 9.49. If our computed test statistic is greater than 9.49, we reject the null hypothesis. This method gives us a clear decision rule for evaluating the presence of a relationship between sex and smoking.

According to the SPSS output, the Pearson Chi-square value is 32.593 with a p-value of .000, which is well below our alpha level of .05. This indicates strong evidence to reject the null hypothesis. However, it’s important to note that 5 cells (55.6%) had expected counts below 5, which slightly violates chi-square assumptions and could impact the accuracy of results. Despite this, the p-value is extremely low, indicating a strong association between sex and smoking status, as seen in the table in this slide.

The test revealed a statistically significant association between sex and smoking behavior. The crosstab shows that females were more likely to be non-smokers or light smokers, while males had higher counts in the moderate smoker category. This gender difference suggests the need for tailored health messaging and targeted interventions. For instance, anti-smoking campaigns might be designed differently for men and women, focusing on their specific motivations and behavioral trends.

These findings have important implications for public health. Acknowledging the differences in smoking behavior between men and women allows for more personalized health education and prevention efforts. For example, anti-smoking campaigns could use messages that resonate more with male audiences who show higher usage. In schools, gender-targeted programming may improve engagement. However, due to the small sample size and assumption violations, further studies with larger samples are needed for generalization.

This analysis had some limitations, particularly the small sample size and multiple cells with expected frequencies below five. These issues can affect the test’s accuracy. While our p-value was significant, we should interpret the findings cautiously. For future studies with small datasets, Fisher’s Exact Test may be more appropriate. Still, the results highlight a pattern worth investigating in a larger sample or through more robust statistical techniques.

To conclude, this analysis demonstrated a significant relationship between sex and smoking status using a chi-square test of independence. Despite a few limitations, the findings highlight the importance of considering gender in smoking prevention efforts. The chi-square test remains a vital tool in public health for analyzing categorical data and guiding intervention planning. Future research with a larger and more balanced sample will help validate these findings and further inform effective health policy.
References
- Aguinis, H., Vassar, M., & Wayant, C. (2021). On reporting and interpreting statistical significance and p values in medical research. BMJ Evidence-Based Medicine, 26(2), 39-42. https://doi.org/10.1136/bmjebm-2019-111264
- Miola, A. C., & Miot, H. A. (2022). Comparing categorical variables in clinical and experimental studies. Jornal Vascular Brasileiro, 21, e20210225. https://doi.org/10.1590/1677-5449.20210225
Place your order now for a similar assignment and get fast, cheap and best quality work written by our expert level assignment writers. Limited Offer: Get 30% OFF Your First Order
Limited Offer: Get 30% OFF Your First Order

Chi-Square Test of Independence
The Chi-Square Test of Independence is a statistical method used to determine whether two categorical variables are related or independent. It is widely used in research to assess relationships in survey data, contingency tables, and other categorical datasets.
What is the Chi-Square Test of Independence?
The Chi-Square Test of Independence (also known as the Pearson Chi-Square Test) is a non-parametric statistical test used to examine whether there is a significant association between two categorical variables.
The test compares the observed frequencies in each category of a contingency table with the expected frequencies, which are calculated under the assumption that there is no association between the variables.
If the observed frequencies are significantly different from the expected frequencies, we reject the null hypothesis and conclude that there is a relationship between the variables.
When Can I Use the Test?
The Chi-Square Test of Independence can be used under the following conditions:
- You have two categorical variables: Each variable should consist of two or more categories. For example, gender (male, female) and preference (like, dislike).
- You have a random sample: The data should be collected using a random sampling method.
- Independence of observations: Each subject or observation should contribute to only one cell in the contingency table.
- Sufficient sample size: Expected frequencies should be at least 5 in most cells. If not, the test may not be valid.
- Data in frequency counts: The data should be in the form of frequency counts, not percentages or proportions.
Can I Use the Test if I Have Frequency Counts in a Table?
Yes, the Chi-Square Test of Independence is specifically designed for data presented as frequency counts in a contingency table. A contingency table shows the frequency distribution of variables and allows you to analyze the relationship between them.
For example, you might have a table like this:
| Likes Product | Dislikes Product | Total | |
|---|---|---|---|
| Male | 30 | 20 | 50 |
| Female | 25 | 25 | 50 |
| Total | 55 | 45 | 100 |
You can use this table directly to apply the Chi-Square Test of Independence.
Using the Chi-Square Test of Independence
Here’s how to conduct the test step-by-step:
1. State the hypotheses
- Null hypothesis (H₀): The two variables are independent (no association).
- Alternative hypothesis (H₁): The two variables are dependent (there is an association).
2. Create a contingency table
Use your data to create a frequency table (e.g., cross-tabulation of gender vs. product preference).
3. Calculate expected frequencies
For each cell in the table:
Expected Frequency=(Row Total)×(Column Total)Grand Total\text{Expected Frequency} = \frac{(\text{Row Total}) \times (\text{Column Total})}{\text{Grand Total}}
4. Compute the Chi-Square statistic
χ2=∑(O−E)2E\chi^2 = \sum \frac{(O – E)^2}{E}
Where:
- OO = observed frequency
- EE = expected frequency
5. Determine degrees of freedom
df=(r−1)×(c−1)df = (r – 1) \times (c – 1)
Where rr = number of rows, cc = number of columns.
6. Find the p-value
Use a Chi-square distribution table or software to find the p-value corresponding to the Chi-square statistic and degrees of freedom.
7. Make a decision
- If p-value < significance level (e.g., 0.05): Reject the null hypothesis — there is a significant association.
- If p-value ≥ significance level: Fail to reject the null — no significant association.
Chi-Square Test of Independence Example
Scenario: A marketing analyst wants to know if product preference is related to gender.
Data collected:
| Likes Product | Dislikes Product | Total | |
|---|---|---|---|
| Male | 30 | 20 | 50 |
| Female | 25 | 25 | 50 |
| Total | 55 | 45 | 100 |
Step 1: Hypotheses
- H₀: Product preference is independent of gender.
- H₁: Product preference depends on gender.
Step 2: Expected frequencies
- Expected (Male, Likes) = (50×55)/100 = 27.5
- Expected (Male, Dislikes) = (50×45)/100 = 22.5
- Expected (Female, Likes) = (50×55)/100 = 27.5
- Expected (Female, Dislikes) = (50×45)/100 = 22.5
Step 3: Compute Chi-Square
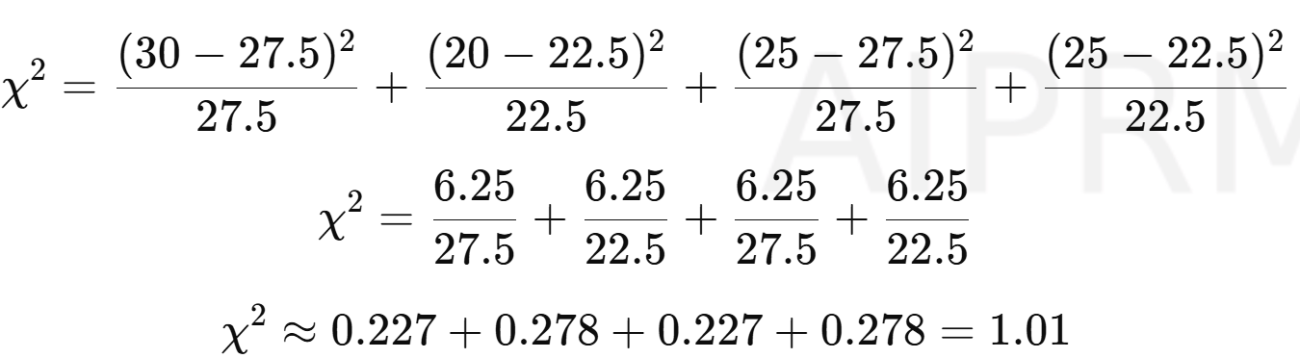
Step 4: Degrees of freedom
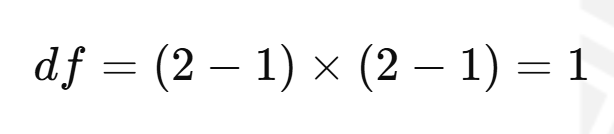
Step 5: Find p-value
Using a Chi-square distribution table or calculator, with df = 1, χ² = 1.01:
- p-value ≈ 0.31
Step 6: Conclusion
Since p-value > 0.05, we fail to reject the null hypothesis. There is no significant association between gender and product preference.
Conclusion
The Chi-Square Test of Independence is a powerful tool for analyzing relationships between categorical variables. It’s simple to apply and interpret when working with frequency data in contingency tables. As long as assumptions are met, this test can provide valuable insights into whether two variables are associated or not.
Whether you’re analyzing survey results, studying consumer behavior, or conducting academic research, mastering this test is essential for effective data analysis in categorical data scenarios.
FAQs

Dan Palmer is a dedicated academic writing specialist with extensive experience supporting nursing students throughout their educational journey. Understanding the unique challenges faced by nursing students who balance demanding clinical rotations, family responsibilities, and rigorous coursework, Dan provides professional assignment assistance that helps students maintain academic excellence without compromising their other commitments.
With a comprehensive understanding of nursing curriculum requirements and academic standards, Dan delivers high-quality, thoroughly researched assignments that serve as valuable learning resources. His expertise spans various nursing disciplines, including clinical practice, healthcare ethics, patient care management, and evidence-based research.
Dan’s approach combines meticulous attention to detail with a commitment to timely delivery, ensuring that busy nursing students receive the support they need when they need it most. His professional assistance has helped countless nursing students successfully navigate their academic programs while maintaining their professional and personal responsibilities.
Committed to academic integrity and excellence, Dan Palmer continues to be a trusted resource for nursing students seeking reliable, professional assignment support.


